量子物性基礎論レポート課題集
・提出期限は目安であり、それを過ぎたら受け取らない、というわけではない。(だけど期限は守って欲しい)
・レポート課題はすべての提出を義務づけるものではない。。。が、首尾良く書かれたのレポート3報以上が単位取得の目安である。
・レポート課題の受理状況はこちらを参照のこと(pdf形式です)(8月24日更新:名前が赤い人は、今のままでは、単位をあげることができない人です。)
・すべてのレポートの最終提出期限は8月6日(月)12:00(西2−307号室レポートボックス)です。→レポート受け取り終了しました(8月24日)。
第一回レポート課題(5月22日出題)
自由電子の状態密度について論ぜよ(1次元、2次元、3次元)。
(次元の違いが状態密度にどのように反映されるか図も示して説明せよ)
第二回レポート課題(6月13日出題)
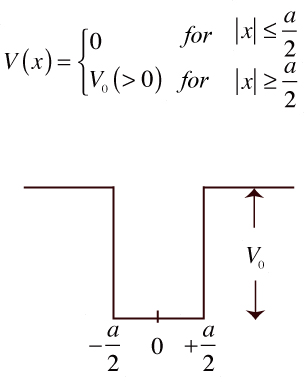
1次元井戸型ポテンシャル(有限高さ障壁)に対するシュレディンガー方程式について、
0<E<V0の束縛状態をグラフを用いて近似的に求める方法を説明せよ。
例えば、V0=0.3 eV, 井戸幅10 nm, 電子の有効質量を真空中のそれの0.067倍(GaAs)だとすると、いくつの束縛状態が可能か?
提出期限:7月11日(水)授業開始「前」
第三回レポート課題(6月13日出題)
1次元井戸型ポテンシャル(有限高さ障壁)に対するシュレディンガー方程式について、
E>V0の非束縛状態(連続状態)について論ぜよ。井戸の左から右へ波が伝播するとき、
どのように量子井戸の影響を受けるか?(キーワード:透過率)
提出期限:7月11日(水)授業開始「前」
第四回レポート課題(6月13日出題)
R.Dingle, W.Wiegmann, and C.H.Henrry, Phys.Rev.Lett. 33, 827 (1974)
"Quantum States of Confined Carriers in Very Thin AlxGa1-xAs-GaAs-AlxGa1-xAs Heterostructures"
を読んで、レポート用紙2〜3枚に内容を要約せよ。
提出期限:7月11日(水)授業開始「前」
第五回レポート課題(6月20日出題)
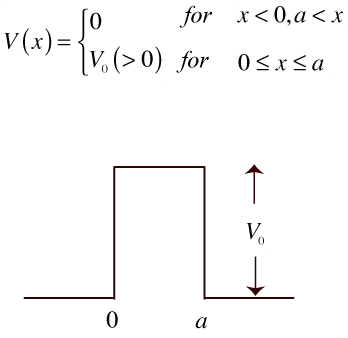
授業中に説明した1次元山型ポテンシャル障壁に対するシュレディンガー方程式について、
0<E<V0の場合について、透過確率と反射確率を求めよ。
提出期限:7月18日(水)授業開始「前」
第六回レポート課題(6月27日出題)
M.Heiblum, M.V.Fischetti, W.P.Dumke, D.J.Frank, I.M.Anderson, C.M.Knoedler, and L.Osterling , Phys.Rev.Lett. 58, 816 (1987)
"Electron Interference Dffects in Quantum Wells: Observation of Bound and Resonant States "
を読んで、レポート用紙2〜3枚に内容を要約せよ。
提出期限:7月25日(水)12:00(提出場所:西2−307ポスト)
第七回レポート課題(6月27日出題)
L.Esaki , Rev.Mod.Phys. 46, 237 (1974)
"Long journey into tunnelling "
を読んで、
(1)トンネルダイオードと負性抵抗(Sec.II & III)
もしくは
(2)共鳴トンネリング(Sec.IV)
の部分を中心にレポート用紙2〜3枚に内容を要約せよ。
提出期限:7月25日(水)12:00(提出場所:西2−307ポスト)
第八回レポート課題(6月27日出題)この課題は必ず提出のこと
各自の研究テーマに関係する量子力学的現象について、自由に問題を設定し
解答せよ。
提出期限:7月25日(水)12:00(提出場所:西2−307ポスト)